Weltzeitalter (dus-bzhi) der tibetischen Zeitrechnung

Die Weltzeitalter (dus-bzhi) bilden den größten Zeitzyklus der tibetischen Zeiteinteilung bzw. Zeitrechnung. Die Länge eines Weltzeitalters wird als der Zeitabschnitt zwischen zwei aufeinanderfolgenden Konjunktionen aller in Tibet bekannten, beweglichen Himmelskörper bzw. Planeten am Nullpunkt der Ekliptik definiert. Außerdem ist dieses Ereignis stets dadurch gekennzeichnet, dass das astronomische Kalenderjahr beginnt und ein bestimmter, sechzig Jahre umfassender Jahreszyklus anfängt. Im Tibetischen wird dieses Ereignis einer großen Konjunktion als stong -´jug „Eintritt ins Leere“ bezeichnet.

Inhaltsverzeichnis

1. Die Weltzeitalter des Kālacakratantra
2. Die Weltzeitalter der tibetischen Astronomie
3. Literatur

1. 1. Die Weltzeitalter des Kālacakratantra

Das Kālacakratantra nennt vier Weltalter, die unterschiedlicher Länge haben, die diese astronomischen Bedingungen erfüllen sollen und die aufeinander gefolgt sind, nämlich das

1.Sanskrit: kṛtyuga, (rdzogs-ldan gyi dus) mit 1.728.000 Jahren, das
2.Sanskrit: tretāyuga, (gsum-ldan gyi dus) .mit 1.269.000 Jahren, das
3.Sanskrit: dvāparayuga, (gnyis-ldan gyu dus) mit 864.000 Jahren und das
4.Sanskrit: kaliyuga, (rtsod-pa'i dus) mit 432.000 Jahren.

2. Die Weltzeitalter der tibetischen Astronomie

Die tibetischen Astronomen des 15. Jahrhunderts fanden nun heraus, dass mit dem im Kālacakratantra vorliegenden Zahlenmaterial von chronologischen Größen und Anfangswerten der Planeten eine große Konjunktion weder in diesen genannten Zeitintervallen noch überhaupt möglich war.

So verwendet das Kālacakratantra als Epoche seiner Zeitrechnung den Beginn des Monats nag zla-ba (Sanskrit: Caitra) des Jahres 806, welches dem 23.3.806 entspricht. Am Beginn dieses Tages stehen nach dem Kālacakratantra Sonne und Mond am Nullpunkt der Ekliptik, welcher mit dem Beginn des Tierkreiszeichens Widder (lug) bzw. des Mondhauses tha-skar zusammenfällt. Das Jahr 806 ist das 20. Jahr des Sechzig-Jahres-Zyklus, der in dem Jahr 787 beginnt.

Da eine große Konjunktion mit dem Beginn am 1. Jahres eines Sechzig-Jahres-Zyklus stattfinden muss und da das Umrechnungsverhältnis von Solar-Monat zu synodischem Monat generell mit

A =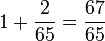  

angegeben wird, bedeutet dies nach den nachprüfbaren Berechnungen der tibetischen Astronomen, dass zu Beginn eines 20. Jahres eines Sechzig-Jahres-Zyklus der Beginn eines synodischen Monats niemals mit dem Beginn eines Solar-Monats zusammenfallen kann.

Umgekehrt gerechnet ergab dies, dass bei Akzeptanz der entsprechenden Werte des Kālacakratantra eine große Konjunktion zu Anfang eines Sechzig-Jahres-Zyklus nicht erfolgen konnte.

Mit dieser und weiterer Kritik an den Anfangswerten errechneten die Astronomen der Phugpa-Schule für die Periode der Eintreffens großer Konjunktionen einen Wert, der im Vaiḍūrya dkar-po des Regenten Desi Sanggye Gyatsho mit 279 623 511 548 502 090 600 Jahren beziffert wurde. Dies sind in Zahlennamen ausgedrückt 279 Trillionen, 623 Billiarden, 511 Billionen, 548 Milliarden, 502 Millionen, 90 Tausend und 6 Hundert Jahre. Die letzte große Konjunktion fand nach dem Vaiḍūrya dkar-po rüchgerechnet vom Beginn des Nag-Monats des Jahres 1687 vor 82 776 132 766 945 179 600 Jahren statt.

Tibetische Quellen berichten davon, dass andere tibetische Astronomen mit verschiedenen Kalkulationsansätzen unterschiedliche Werte für die Länge eines Weltzeitalters berechneten.

Literatur

Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig Maximilians Universität zu München. München 1966
Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973

Autor: Dieter Schuh, 2010