 | |  |
Das Gesicht des sGra-gcan genannten Ungeheuers, welches Sonne und Mond verschlingt. Quelle: Vaiḍūrya dkar-po | | Das Symbol für den sGra-gcan als Planet: Ein Vogelkopf. Quelle: Himalayan Art Resources, http://www.himalayanart.org/image.cfm/28.html |
Sonnenfinsternis (nyi-´dzin) und Mondfinsternis (zla-´dzin)
Nach den von den Tibetern aus Indien übernommenen Vorstellungen kreist in der gemeinsamen Umlaufbahn der Sonne, des Mondes und der Planeten um den Weltberg ein sGra-gcan genanntes Ungeheuer. Dieses verschlingt ganz oder teilweise die Sonne und den Mond, wenn es mit seinem Kopf oder Schweif zu den Zeitpunkten des Vollmonds bzw. des Neumonds ihnen zu nahe kommt. Diese mythologische Betrachtungsweise hat einen astronomischen Grund. Kopf bzw. „Gesicht“ und Schweif des sGra-gcan repräsentieren die sogenannten Mondknoten, d.s. die Schnittpunkte der Ebene der scheinbaren Sonnenbahn mit der Ebene der Mondbahn. Nach der Übersetzung des indischen „Tantra vom Rad der Zeit“ (Kālacakratantra), das auch ein Kapitel über Astronomie und Zeitrechnung enthält, entwickelte sich nach dem 11. Jahrhundert in Tibet eine Astronomie, die auch die Aufgabenstellung übernahm, Sonnen- und Mondfinsternisse zu berechnen und somit vorherzusagen. Die Grundlage hierzu war die Berechnung der ekliptikalen Längen der Mondknoten, für deren Umlaufzeit der relativ zuverlässige Wert von 18,6 Jahre angenommen wurde.
Angesichts der Kompliziertheit der Berechnungen von Sonnen- und Mondfinsternissen ist es nicht verwunderlich, dass die tibetischen Astronomen mit ihrem einfachen Modell des Aufbaus von Himmel und Erde häufig nicht zutreffende Vorhersagen über das Eintreffen von Finsternissen abgaben. Die Vorausberechnungen dieser Ereignisse, die zeitweise sogar durch öffentliche Anschläge im Voraus bekannt gegeben wurden, waren zweifellos eine dauernde Quelle von Frustration für die tibetischen Gelehrten auf dem Gebiet der Astronomie. Gleichwohl ist es ein bemerkenswertes Phänomen der traditionellen tibetischen Kultur, dass man auf der Grundlage indischer Traditionen bis in die Neuzeit – teilweise auch erfolgreich – mittels Berechnungen auf dem Sandabakus immer wieder versuchte, die mit der Vorhersage von Finsternissen verbundene schwierige Aufgabenstellung zu lösen.
Für das religiöse Leben der Tibeter waren Sonnen- und Mondfinsternisse von herausragender Bedeutung. Verdienste, die man während solcher Ereignisse erwarb, potenzierten sich zehnmillionenfach, weshalb die Gläubigen aufgefordert wurden, bei solchen Finsternissen sich entsprechenden religiösen Aktivitäten zu widmen. Allerdings wurden nach dem Glauben der Tibeter auch schlechte Taten entsprechend potenziert. Aus diesen Gründen war das öffentliche Interesse an einer korrekten Vorhersage der Finsternisse stets sehr groß.
Inhaltsverzeichnis
1. Vorbemerkungen zu den astronomischen Grundlagen von Sonnen- und Mondfinsternissen
2. Tibetische Berechnungen der Längen der Mondknoten
3. Tibetische Berechnungen der Finsternisse aus dem Vergleich der Längen der Mondknoten mit den geozentrischen, ekliptikalen Längen von Sonne und Mond
4. Literatur
1. Vorbemerkungen zu den astronomischen Grundlagen von Sonnen- und Mondfinsternissen
Wie im Zusammenhang mit der Darstellung der tibetischen Kalenderrechnung ausführlich erläutert wurde, sind die sogenannten Mondphasen für die tibetische Einteilung der Zeit von außerordentlicher Bedeutung. Die Länge eines tibetischen Monats ist die Zeitspanne zwischen zwei Neumonden, und die Tage des tibetischen Kalenders sind so geordnet, dass Vollmond sich stets am 15. Kalendertag ereignet.
Astronomisch gesehen findet Neumond immer dann statt, wenn der Mond zwischen der Erde und der Sonne steht, die geozentrischen Längen des Mondes und der Sonne also gleich sind. Die der Erde zugewandte Seite des Mondes wird nicht von der Sonne beschienen und ist somit von der Erde aus nicht sichtbar. Vollmond findet dann statt, wenn die Erde genau zwischen der Sonne und dem Mond steht, d. h. dass die geozentrischen Längen des Mondes und der Sonne sich somit genau um 180 Grad unterscheiden. Die Entstehung der verschiedenen Mondphasen ist anhand der folgenden Darstellung gut zu verstehen, wobei die gelben Pfeile den Einfall des Sonnenlichtes darstellen.
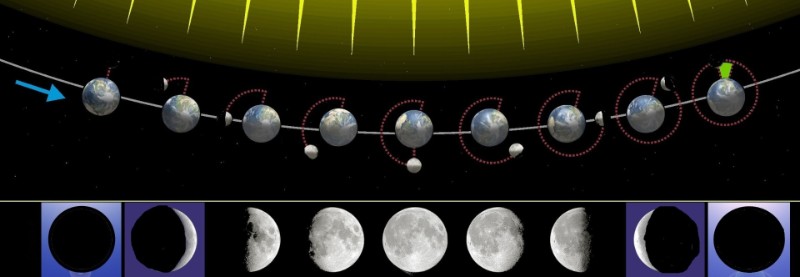 |
Nicht maßstabgerechte Darstellung der Bewegung des Mondes um die Erde, die sich ihrerseits von links nach rechts bewegt. Die Positionen des Mondes sind anhand der rot gestrichelten Linien auszumachen. In der ersten und letzten der dargestellten Positionen ist der Mond von der Erde aus nicht sichtbar. Leicht abgeänderte Quelle: Wikipedia, Urheber Orion 8. http://en.wikipedia.org/wiki/File:Moon_phases_en.jpg |
Steht der Mond bei Vollmond nun gleichsam hinter der Erde, so stellt sich die Frage, warum der Erdschatten nicht zeitweise verhindert, dass überhaupt Sonnenlicht die Mondoberfläche erreicht und somit, von der Erde aus gesehen, nicht jedes Mal am 30. Tag eines tibetischen Monats eine Mondfinsternis stattfindet. Das Ereignis einer Mondfinsternis wird anhand des folgen Bildes deutlich gemacht, welches natürlich nicht maßstabsgerecht ist.
An dieser Stelle ist anzumerken, dass sich die verschiedenen Planeten nicht genau in einer Ebene um die Sonne bewegen. Das Gleiche gilt für die Ebenen, die die Umlaufbahn des Mondes um die Erde und die Umlaufbahn der Erde um die Sonne bilden. Steht also der Mond im Verhältnis zu der Außenhülle des oben abgebildeten Schattenkegels der Erde (Umbra) oberhalb oder unterhalb, so ist er voll von der Erde aus sichtbar und eine Mondfinsternis findet nicht statt.
Um die Bewegung des Mondes in der Breite zu erläutern, sei im Folgenden eine Darstellung der Bahnebenen von Sonne und Mond aus der Sicht eines Beobachters auf der Erde vorgestellt. Auf dieser Abbildung sieht man zwei Punkte N1 und N2. Dies sind die Schnittpunkte der Mondbahn mit der Ebene der Sonnenbahn. Sie werden Mondknoten genannt. Wenn der Mond diese Punkte durchläuft, befindet er sich mit der Erde und der Sonne in einer Ebene. Aufgrund der dem Mond eigenen Himmelsmechanik drehen sich die Ebenen von Sonne und Mond gegeneinander. Dies bedeutet aus der Sicht der Erde, dass sich die Punkte N1 und N2 gegen den Uhrzeigersinn (also im Verhältnis zu den Planeten und zur Sonne in umgekehrter Richtung) bewegen und in 18,61 Jahren einen vollen Umlauf in der Ekliptik hinter sich bringen. Befindet sich nun der Mond bei Vollmond oder Neumond in der Nähe eines dieser beiden Mondknoten, so kann für einen Beobachter auf der Erde eine Mondfinsternis oder Sonnenfinsternis stattfinden.
2. Tibetische Berechnungen der ekliptikalen Längen der Mondknoten
Sonnen- und Mondfinsternisse werden im Tibetischen als nyi-´dzin „Ergreifen der Sonne“ und zla-´dzin „Ergreifen des Mondes“ bezeichnet. Für ihre Berechnung ist die Kalkulation der Mondknoten eine Voraussetzung. Winfried Petri war der erste, der entdeckte, dass sich im Kālacakratantra Angaben zur Berechnung der Mondknoten finden, die nach der indischen Tradition als Rāhu und Ketu bezeichnet werden. Petri schreibt hierzu (S. 142): „ Rāhu und der nicht immer von ihm selbstständig unterschiedene Ketu spielen im Kālacakratantra zunächst die gleiche Rolle wie in der allgemeinen indischen Lehre. Sie verschlingen bei Tag, in der dunklen Monatshälfte (Neumond), die Sonne und bei Nacht, in der lichten Monatshälfte (Vollmond), den Mond (Kālacakratantra 86).“
Petri errechnete für die im Kālacakratantra mit 460 halbe synodische Monate angegebene Umlaufzeit der Mondknoten den Zeitraum von 18,6 Jahre, was dem modernen Wert von 18,61 Jahren sehr nahe kommt. Der Abstand der Knoten in der Ekliptik beträgt 180 Grad. In der tibetischen astronomischen Literatur wurde für die Umlaufzeit dieses sich zwischen den beiden Mondknoten erstreckenden, sGra-gcan genannten Ungeheuers, das Sonne und Mond verschlingt, generell der Wert des Kālacakratantra übernommen. In den Berechnungen wird der erste Knoten als gdong „Gesicht“ und seine berechnete ekliptikale Länge als gdong-skar "Sternort des Gesichts" bezeichnet. Der zweite Knoten wird als mjug „Schweif“ oder dus-me erwähnt.
Die Berechnungen der Längen der Mondbahnknoten wurden in der tibetischen Astronomie nur für das Ende des 15. und das Ende des 30. lunaren Tages (tshes-zhag) eines Monats durchgeführt, weil die Länge der Mondknoten natürlich nur im Hinblick auf den jeweiligen Vollmondstag und den Neumondstag interessierten. Grundlage aller Kalkulationen war die im Kālacakratantra überlieferte Umlaufzeit (dkyil-´khor) von 460 halben Monaten (sgra-can tshes-zla phyed-pa´i dkyil-´khor), was wiederum einer Umlaufzeit von 230 vollen synodischen Monaten (sgra-gcan tshes-zla´i dkyil-´khor) entspricht. Multipliziert man diese Zahl mit 30 so erhält man als Umlaufzeit der Mondknoten in lunaren Tagen (sgra-gcan tshes-zhag dkyil-´khor) den Betrag 6900. Teilt man nun das Winkelmaß für einen vollen Umlauf, d.s. 27 rgyu-skar, durch 6900, so erhält man mit W = [0,0,14,0,12]/(27,60,60,6,23) den Betrag (longs-spyod) für die Veränderung der Länge der Mondknoten pro lunarem Tag (sgra-gcan tshes-zhag gi rtag-longs). Dieser Betrag wird z. B. vom Regenten Sangs-rgyas rgya-mtsho in seinem 1685 fertig gestellten Vaiḍūrya dkar-po verwendet.
Die Berechnung der ekliptischen Längen der Mondknoten wird im Prinzip analog zu dem bei der Berechnung der mittleren Längen der Planeten angewendeten Verfahren durchgeführt (siehe Tibetische Astronomie, 7.1. und 7.3). Insofern hier die Umlaufzeit in synodischen Monaten angegeben ist, geht man aber nun von der Zahl der seit der Epoche vergangenen synodischen Monate L (zla-dag) aus und addiert als Anfangswert (Anf) die Zahl der synodischen Monate, die der als gdong ("Gesicht") bezeichnete Mondknoten benötigt hat, um nach Durchlauf durch den Nullpunkt der Ekliptik seine Länge zum Zeitpunkt der Epoche zu erreichen. Die Rechnung ⌊(Anf +L):230⌋• 30 ergibt nun die Anzahl der lunaren Tagen, die zum jeweiligen Beginn des letzten Monats seit dem letzten Durchlauf des Knotens durch den Nullpunkt der Ekliptik vergangen sind. Addiert man 15 so erlangt man diesen Wert für das Ende des Vollmondtages des laufenden Monats. Addiert man 30 erlangt man diesen Wert für das Ende des Neumondtages des laufenden Monats. Die Multiplikation der Ergebnisse mit W = [0,0,14,0,12]/(27,60,60,6,23) mod 27 ergibt nun einen Wert für das „Gesicht“ des sGra-gcan. Dieser Wert wird als rtsa-ba bezeichnet. Dass es sich hierbei noch nicht um die zu berechnende Länge des Mondknotens handelt, liegt einfach an Folgendem: Man hat bei dieser Rechnung wohl aus praktischen Gründen so getan hat, als würde sich der Mondknoten in dieselbe Richtung bewegen, wie die übrigen Planeten, also bezogen auf die übliche Darstellung der Mondhäuser gegen den Uhrzeigersinn bzw. astronomisch gesprochen von Westen nach Osten. Da aber nunmehr hier das Gegenteil der Fall ist, ist noch eine einfache Korrektur erforderlich. Man subtrahiert von dem Winkel eines vollen Umlaufs, also von 27 rgyu-skar, einfach den errechneten Wert (rtsa-ba). Das Ergebnis ist die Länge (gdong-skar bzw. gdong-gnas skar) des „Gesichts“ bzw. „Kopfes“ des sGra-gcan. Addiert man zu diesem Ergebnis den Betrag eines halben Umlaufs (´khor-phyed), also 13 rgyu-skar und 30 chu-tshod, so erhält man die ekliptikale Länge des mjug oder dus-me genannten zweiten Mondknotens.
Schon im Kālacakratantra findet sich die Darstellung einer leicht abweichenden Methode der Berechnung der Mondknoten, die aber zum gleichen rechnerischen Ergebnis führt. Diese Methode wurde schon von Petri (S. 142) beschrieben, wobei dieser aber die erforderliche Subtraktion von 27 ausließ. Man rechnet hierbei mit Halbmonaten und verwendet deshalb für die Umlaufzeit der Mondknoten den Betrag von 460 Halbmonaten. Da stets nur die Längen der Mondknoten zum Ende des 15. und 30. lunaren Tages berechnet werden, ergibt sich die ekliptikale Länge des Gesichts des sGra-gcan (gdong-skar) nach den Formeln
27-⌊(Anf +L•2+1):460⌋•(27:460) bzw.
27-⌊(Anf +L•2+2):460⌋•(27:460).
3. Tibetische Berechnungen der Finsternisse aus dem Vergleich der ekliptikalen Längen der Mondknoten mit den geozentrischen, ekliptikalen Längen von Sonne und Mond
Nach der tibetischen Vorstellung ergreift nun der sGra-gcan am Ende des 15. oder 30. lunaren Tages entweder den Mond oder die Sonne, wenn der Abstand zwischen seinem „Gesicht“ oder seinem „Schweif“ und den ekliptikalen Positionen von Mond und Sonne hinreichend klein ist. Da den Tibetern natürlich aus der Beobachtung bekannt war, dass es z. B. totale und partielle Sonnen- und Mondfinsternisse gab, versuchten sie, Vorhersagen über das Eintreffen und die Art der Sonnen- und Mondfinsternisse aus den Differenzen der Längen der Mondknoten einerseits und der Sonne bzw. des Mondes andererseits abzuleiten. Es ist bemerkenswert, dass die ersten aus dem Indischen ins Tibetische übersetzten Werke mit astronomischen Inhalten, wie das Kālacakratantra, das Kālacakrāvatāra bzw. die Vimalaprabhā keine näheren Erläuterungen dieser Berechnungen enthalten. Allerdings stammen die ersten uns bekannten Kalkulationen hierzu wiederum aus Indien und erreichten Tibet zu Beginn des 13. Jahrhunderts. Sie liegen uns mit einer kleinen Schrift aus der Feder des oben berühmten kaschmirischen Gelehrten Śākyaśrībhadra vor, der während seines langen Aufenthaltes in Tibet (1204 – 1214) auch als Lehrer des Sakya Pandita Künga Gyeltshen (Kun-dga´ rgyal-mtshan) wirkte. Die kleine Schrift trägt in der sDe-dge-Ausgabe des Tanjur (bsTan-´gyur) den Titel Nyi-zla ´dzin-pa´i rtsis „Berechnung der Sonnen- und Mondfinsternisse“. Im Kolophon wird sie als Dus kyi ´khor lo rtsis kyi man-ngag „Besondere Unterweisung über die Astronomie des Kālacakra“ aufgeführt. Sie beschreibt im ersten Teil die Berechnung der Mondknoten nach der oben beschriebenen zweiten Methode und erläutert in einem zweiten Teil, wie man unter Einbeziehung der siderischen Längen von Sonne und Mond berechnen kann, ob und wann sich Sonnen- und Mondfinsternisse ereignen und ob es sich um totale oder partielle Finsternisse handelt. Des Weiteren werden auch der genaue Zeitpunkt und die zeitliche Dauer der Sonnen- und Mondfinsternisse behandelt.
Das erste uns bisher bekannt gewordene, von einem tibetischen Gelehrten geschriebene Werk, welches sich mit diesem Thema beschäftigte, wurde 1318 von karma Rangjung Dorje (Rang-byung rdo-rje) verfasst und trägt den Titel rTsis kyi bstan-bcos kun las btus-pa´i rtog-pa. Im 10. Kapitel behandelt dieses Werk unter dem Titel Ñi-ma zla-ba la dgra-gcan ´jug-pa „Eintreten des sGra-gcan in Sonne und Mond“ die gleiche Thematik wie Śākyaśrībhadra in seinem Ñi-zla ´dzin-pa´i rtsis. Die Berechnungen von karma Rangjung Dorje unterscheiden sich auf den ersten Blick erheblich von denen des Śākyaśrībhadra. Überhaupt trifft dies auch für fast alle späteren Werke zu, die die Sonnen- und Mondfinsternisse behandeln. Der Grund für diese zum Teil erheblich unterschiedlichen Darstellungen liegt darin, dass die tibetischen Astronomen mit ihren Vorhersagen der Sonnen- und Mondfinsternisse nicht sehr erfolgreich waren. Dieses Versagen der tibetischen Astronomie im Hinblick auf zuverlässige Vorhersagen der Sonnen- und Mondfinsternisse führte dazu, dass man immer wieder versuchte, durch Veränderung der Berechnungsmethoden bessere Ergebnisse zu erzielen. In diesem Zusammenhang spricht man von Kalkulationen, die auf Erfahrung beruhen (myong-rtsis). Die wissenschaftliche Untersuchung der Geschichte der Berechnung der Sonnen- und Mondfinsternisse in Tibet ist eines der wichtigen Desiderata in der Erforschung der tibetischen Astronomie.
Um einen Eindruck von den Verfahren zu vermitteln, die die tibetischen Astronomen z. B. zur Berechnung der Mondfinsternisse anwendeten, seien hier die entsprechenden Darlegungen des Werkes Rigs-ldan snying gi thig-le vorgestellt, welches von dem ca. 1882 geborenen Khyenrab Norbu (mKhyen-rab nor-bu) im zweiten Viertel des 20. Jahrhunderts verfasst wurde. Khyenrab Norbu ermittelt zunächst die Differenzen zwischen der nach der grub-rtsis berechneten ekliptikalen Länge des Mondes (tshes-´khyud zla-ba´i skar-ma) am Ende des 15. lunaren Tages und den Längen der beiden Mondknoten für den gleichen Zeitpunkt. Ist in einer dieser Differenzen der Sternort (rgyu-skar) = 0 und der Betrag in der Stelle der chu-tshod kleiner gleich 50, soll nach Khyenrab Norbu stets eine Mondfinsternis stattfinden. In diesem Fall dividiert man diesen Betrag in der Stelle der chu-tshod durch 5 und benutzt mit dem Ergebnis (ohne Rest) dieser Division (nor-grangs) als Zugriffszahl die folgende Tabelle, um darin die Größe und die Dauer der Mondfinsternis abzulesen.
Je nachdem, ob das Ereignis sich am Mondknoten „Gesicht“ (gdong) oder „Schweif“ (mjug oder dus-me) des sGra-gcan ereignet, werden für die Dauer (sgrib-yun) unterschiedliche Zeitspannen angegeben.Khyenrab Norbu gibt zusätzlich auch Hinweise zu der Richtung, aus der die Verfinsterung erfolgt, und Erläuterungen zu den unterschiedlichen Farben, die der Mond nach Eintritt der Mondfinsternis annimmt.

|
Tibetische Tabelle zur Bestimmung der Größe und der zeitlichen Dauer von Mondfinsternissen |
| Zugriffszahl | 1, 2, 3 | 4 | 5 | 6 |
| Größe | Totale Finsternis | Die Ränder des Mondes sind hellgrau | 1/6 bleibt unverdeckt | 2/3 werden verdeckt |
| Dauer am Knoten „Gesicht“ | 16 chu-tshod und 0 chu-srang | 15 chu-tshod und 48 chu-srang | 13 chu-tshod und 20 chu-srang | 11 chu-tshod und 0 chu-sra$ |
| Dauer am Knoten „Schweif“ | 15 chu-tshod und 0 chu-srang | 14 chu-tshod und 38 chu-srang | 12 chu-tshod und 30 chu-srang | 10 chu-tshod und 0 chu-srang |
| Zugriffszahl | 7 | 8 | 9 | 10 |
| Größe | ½ wird verdeckt | 1/3 (wird verdeckt) | 1/6 (wird verdeckt) | 1/8 (wird verdeckt) |
| Dauer am Knoten „Gesicht“ | 8 chu-tshod und 0 chu-srang | 5 chu-tshod und 20 chu-srang | 2 chu-tshod und 40 chu-srang | 2 chu-tshod und 0 chu-srang |
| Dauer am Knoten „Schweif“ | 7 chu-tshod und 20 chu-srang | 5 chu-tshod und 0 chu-srang | 2 chu-tshod und 30 chu-srang | 1 chu-tshod, 52 chu-srang und 3 dbugs |
Im Hinblick auf die Sonne werden vergleichbare Berechnungen für das Ende des 30. lunaren Tages durchgeführt, wobei Khyenrab Norbu hier von den Differenzen zwischen der geozentrischen Länge der Sonne (nyi-dag) und den ekliptikalen Längen der beiden Mondknoten ausgeht.
4. Literatur
Kālacakratantra: Tibetischer Titel: mChog gi dang-po sangs-rgyas las phyung-ba rgyud kyi rgyal-po dus kyi ´khor-lo. The Tibetan Tripitaka, Peking Edition, Tokyo-Kyoto 1955-1961, Bd. 1, Nr. 4
Kālacakrāvatāra: Tibetischer Titel: Dus kyi ´khor-lo la ´jug-pa. The Tibetan Tripitaka, Peking Edition, Tokyo-Kyoto 1955-1961, Bd. 47, Nr. 2098
mKhyen-rab nor-bu: bsTan-bcos vaiḍūrya dkar-po dang nyin-byed snang-ba´i dgongs-don gsal-bar ston-pa rtsis-gzhi´i man-ngag rigs-ldan snying gi thig-le. Nachdruck Dharmsala 1968
Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig Maximilians Universität zu München. München 1966
karma Rang-byung rdo-rje: rTsis kyi bstan-bcos kun las btus-pa´i rtog-pa. Blockdruck, 27 Blatt
Śākyaśrībhadra: Nyi-zla ´dzin-pa´i rtsis. The Tibetan Tripitaka, Peking Edition, Tokyo-Kyoto 1955-1961, Bd. 47, Nr. 2210
Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973
Dieter Schuh: Grundzüge der Entwicklung der Tibetischen Kalenderrechnung. Zeitschrift der Deutschen Morgenländischen Gesellschaft, Supplement II. XVIII. Deutscher Orientalistentag vom 1. bis 5. Oktober 1972 in Lübeck. Vorträge, S. 554-566
Vimalaprabhā:Tibetischer Titel: Dri-med ´od-zer. The Tibetan Tripitaka, Peking Edition, Tokyo-Kyoto 1955-1961, Bd. 46, Nr. 2064
Vaiḍūrya dkar-po: Phug-lugs rtsis kyi legs-bshad mkhas-pa'i mgul-rgyan vaidur dkar-po'i do-shal dpyod-ldan snying-nor (Blockdruck)
Autor: Dieter Schuh, 2011





