Tibetische Astronomie (skar-rtsis)
Die tibetische Astronomie (skar-rtsis, „Kalkulation der Stern(orte)“) ist die im historischen Tibet verbreitete Wissenschaft (rig-gnas; „Ort des Wissens“) über den Aufbau der Erde und des Weltalls, über die Kalenderrechnung genannte Errechnung der Struktur und der Bestandteile des tibetischen astronomischen Kalenders, über die Berechnung der Bewegung der in Tibet bekannten zehn Planeten einschließlich der Sonne, des Mondes, der Mondbahnknoten sowie des Kometen Enckeund über die Berechnung von Sonnen- und Mondfinsternissen. Durchgeführt wurden die astronomischen Berechnungen mit dem tibetischen Sandabakus.
Die Tibetische Astronomie und ihre Berechnungen werden auch heute noch sowohl in Tibet als auch außerhalb Tibets zur Erstellung des jährlichen Kalenders praktiziert.
Inhaltsverzeichnis
1. Geschichte
2. Aufbau der Erde und des Sternhimmels
3. Ekliptik und Winkelmaße
4. Rechenmethoden in der tibetischen Astronomie
5. Zeitrechnung
6. Mittlere Umlaufzeiten von Sonne und Mond sowie der fünf Planeten Merkur, Venus, Mars, Jupiter und Saturn
6.1. Die zeitlichen Längen von lunarem Tag und Zodiak-Tag
6.2. Siderische Umlaufzeit und Winkelgeschwindigkeit der Sonne
6.3. Umlaufzeit und Winkelgeschwindigkeit des Mondes
6.4. Untere und obere Planeten
6.5. Umlaufzeiten der Planeten Merkur, Venus, Mars, Jupiter und Saturn
7. Mittlere ekliptikale Längen der Planeten Merkur, Venus, Mars, Jupiter und Saturn
7.1. Zahl der seit Epoche vergangenen natürlichen Tage
7.2. Anfangswerte
7.3. Mittlere Längen der fünf Planeten
8. Die langsamen Füße der Planeten: siderische Mittelpunktsgleichungen
9. Die schnellen Füße der fünf Planeten: Berechnung der geozentrischen Abweichungen der Längen der Planeten
10. Literatur
1. Geschichte
Hauptartikel siehe Tibetische Astronomiegeschichte
Die tibetische Astronomie ist indischen Ursprungs, da sie auf den astronomischen Lehren des ersten Kapitels des Kālacakratantra beruht, eines indischen tantrischen Lehrtexts, dessen Sanskrit-Textversion nicht vor 1027 entstanden sein kann und der in der 2. Hälfte des 11. Jahrhunderts erstmals ins Tibetische übersetzt wurde.
Die im Kālacakratantra enthaltenen astronomischen Berechnungen entsprechen dem, was in zahlreichen praktischen Rechenbüchern der indischen Astronomie und Kalenderrechnung üblicherweise dargestellt wurde. In Sanskrit werden solche Rechenbücher Karaņa bzw. später im Tibetischen byed rtsis („Praktisches Rechnen“) genannt. Die verwendeten Rechengrößen wurden zur Erleichterung der praktischen Durchführung der Rechnungen in solchen Werken verkürzt bzw. aufgerundet.
 | |  | |  |
Der Astronom Phugpa Lhündrub Gyatsho (1. Hälfte des 15. Jahrhunderts) | | Der Astronom Norsang Gyatsho (2. Hälfte des 15. Jahrhunderts) | | Der Regent und Astronom Sanggye Gyatsho (17. Jahrhundert) |
Ausgangspunkt der Entwicklung einer eigenen tibetischen Astronomie war die in dem kanonischen Text Vimalaprabhā, einem Kommentar zum Kālacakratantra, verbreitete These, Ungläubige hätten die wahre, vom Buddha gelehrte und in einem verlorengegangenen Wurzel-Tantra (rtsa-rgyud) aufgezeichnete Astronomie in böswilliger Absicht verfälscht und diese Verfälschungen im ersten Kapitel des Kālacakratantra verbreitet.
Die Aufgabenstellung der tibetischen Astronomen wurde somit von ihnen selbst letztendlich als „Rekonstruktion der wahren, von Buddha gelehrten Siddhānta-Astronomie“ verstanden, die im Tibetischen als grub-rtsis bezeichnet wurde. Beobachtungen des Sternhimmels waren eigentümlicher Weise für die Entwicklung dieser Astronomie ohne nennenswerte Bedeutung.
Im 15. Jahrhundert bildeten sich in Tibet verschiedene Schultraditionen der Astronomie heraus. Die bekanntesten von ihnen waren die Phug-pa-Schule und die mTshur-phu-Schule.
2. Aufbau der Erde und des Sternhimmels
Hauptartikel siehe Tibetische Kosmographie
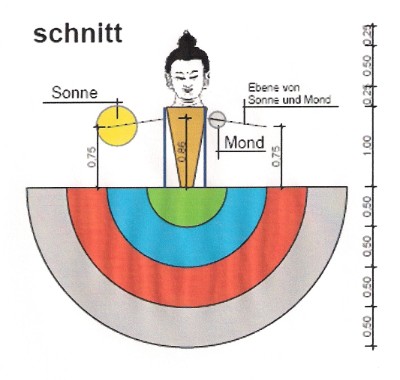
Die Erde wird als Halbkugel vorgestellt. Sie besteht aus vier Kugelschalen, die materialmäßig aus einem der Elemente Luft, Feuer, Wasser und Erdreich bestehen. Hierbei bildet die Luft die äußere Halbkugel, auf die Feuer, Wasser und der aus Erde bestehende Kern folgen. Aus der ebenen Schnittfläche dieser Halbkugel ragt inmitten des aus Erde bestehenden Kerns der runde Weltberg (ri-rab, lhun-po) empor.
Um den Weltberg bewegen sich auf dem Mantel eines Kegelstumpfes Sonne, Mond und die Planeten. Während sich die Fix-Sterne über die ganze Himmelshalbkugel verteilen, die sich im Uhrzeigersinn angetrieben durch einen Treibwind einmal pro Tag um den Weltberg dreht, besitzen Sonne, Mond und Planeten zusätzlich eine Eigenbewegung (rang-'gros) die bewirkt, dass sich diese Himmelskörper mit unterschiedlicher Geschwindigkeit zusätzlich gegen den Uhrzeigersinn um den Weltberg bewegen.
3. Ekliptik und Winkelmaße
Hautartikel siehe Tibetische Mondhäuser
Hauptartikel siehe Tibetische Tierkreiszeichen
Hauptartikel siehe Tibetische Winkelmaße
Der Großkreis, der durch die Projektion der scheinbaren Bahn der Sonne in Verlauf eines Jahres auf der Himmelskugel entsteht wird Ekliptik genannt. Auf ihm bewegen sich vom Standpunkt der Erde aus gesehen bei geringfügigen Abweichungen in der sogenannten Breite, alle Planeten einschließlich des Mondes
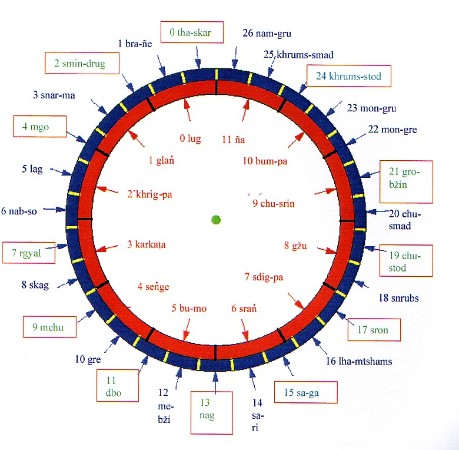
Die erste Aufteilung dieses Großkreises in Tibet ist die in 12 Tierkreiszeichen, die tibetisch als khyim bezeichnet wurden. Für die astronomischen Berechnungen wurden sie mit den Zahlen 0 bis 11 gezählt und bezeichnet. Das Gleiche gilt für die Einteilung der Ekliptik in die sogenannten 27 Mondhäuser bzw. Mondstationen, die tibetisch als rgyu-skar bezeichnet wurden und die, wie auf der Abbildung links unten in blauer Farbe dargestellt ist, von 0 bis 26 gezählt wurden.
Die Bogen- bzw. Winkelmaßeinheit rgyu-skar wurde in 60 chu-tshod „Bogenstunden“ unterteilt. Die chu-tshod wurden in 60 chu-srang „Bogenminuten“ unterteilt. Eine chu-srang bestand aus 6 dbugs „Bogenatemzug“, die wiederum in „Teile“ (cha-shas) mit zum Teil unterschiedlicher Größe unterteilt wurden. Es wird deutlich, dass mit diesem System von Winkelmaßen die ekliptikalen Längen von Sonne, Mond und der Planeten sehr genau bestimmt werden konnten.
4. Rechenmethoden in der Tibetischen Astronomie
Hauptartikel siehe Tibetischer Sandabakus
Die astronomischen Berechnungen der Tibeter wurden auf dem Sandabakus durchgeführt. Die entsprechenden Rechenanweisungen, die den Kern der tibetischen Darstellungen astronomischer Berechnungen bilden, gleichen heutigen Computerprogrammen. Die Besonderheit ist, dass lineare Gleichungen zur Berechnung der ekliptikalen Längen von Planeten, zeitlichen Größen und der Mittelpunktsgleichungen von Himmelskörpern ausschließlich als Programmtexte zur Durchführung von Berechnungen auf dem Sandabakus formuliert wurden. Die Lösung mathematischer Aufgabenstellungen durch das Denken in den Programmstrukturen des Sandabakus ist eine Besonderheit der tibetischen Mathematiker und Astronomen.
Die Zahlenwerte einer Größenangabe, bei der man nicht dem Dezimalsystem folgt, werden auf dem Sandabakus untereinander geschrieben. Die an der jeweiligen Stelle notierte Zahl ist in der tibetischen Astronomie bzw. beim Rechnen auf dem Sandabakus stets eine ganze Zahl. Die Stellen sind stets übereinander platziert, also zum Beispiel für 3 rgyu-skar, 26 chu-tshod, 5 chu-srang und 4 dbugs:
Die Stellenwerte sind in diesem Beispiel (von oben nach unten) 27, 60, 60 und 6. Sie werden in Tibet nicht gesondert notiert.
Um solche Zahlen raumsparender wiederzugeben, werden im Folgenden die Zahlgrößen in eckigen Klammern mit Kommata getrennt notieren und die Stellenwerte dahinter durch einen Schrägstrich getrennt in runden Klammern angegeben. Der vorstehende Zahlenwert wird also als [3,26,5,4]/(27,60,60,6) wiedergegeben. Allgemein gesprochen werden im Folgenden solche, meist fünfstellige Zahlen als [a1,a2,a3,a4,a5]/(st1,st2,st3,st4,st5) geschrieben, wobei an Ganze Zahlen und stn die Stellenwerte sind.
Als besondere Schreibeweise wird mit 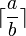 das Ergebnis der Division zweier Ganzer Zahlen ohne Rest und mit
das Ergebnis der Division zweier Ganzer Zahlen ohne Rest und mit  der Rest dieser Division bezeichnet.
der Rest dieser Division bezeichnet.
5. Zeitrechnung
Hauptartikel siehe Tibetische Kalenderrechnung
Für die tibetische Zeitrechnung ordnet sich das Weltgeschehen zeitlich in zyklischen Strukturen. Dabei sind die Zeiteinheiten dieser Zyklen in der Regel durch astronomische Phänomene definiert. Das Weltzeitalter beginnt und endet mit dem Zusammentreffen aller Planeten am Nullpunkt der Ekliptik, das Jahr ergibt sich aus der Vollendung der scheinbaren Umdrehung der Sonne um die Erde, der Monat beschreibt die Zeitspanne zwischen zwei Neumonden und der Kalendertag ist der natürliche Tag.
 |
Tibetischer Kalender: Beginn des 3. Hor-Monats im tibetischen Kalender aus Lhasa für das Wasser-Schwein Jahr 1923/24 |
Der mit der astronomischen Kalenderrechnung erstellte Almanach ist ein lunisolarer Kalender.
Im Zentrum der tibetischen Zeitrechnung steht die Berechnung des Datums (lunarer Tag) innerhalb eines Monats, mit dem ein natürlicher Tag bzw. Wochentag innerhalb eines Monats gezählt wird. Des Weiteren werden für jeden Wochentag die ekliptikalen Längen von Sonne und Mond sowie zwei weitere astrologisch bedeutsame Größen berechnet, die als byed-pa (Sanskrit: karaṇa) und sbyor-ba (Sanskrit: yoga) bezeichnet werden. Da die Rechnungen auf die Feststellung dieser fünf Komponenten hinauslaufen, wird die Kalenderrechnung auch als yan lag lnga bsdus „Zusammenfassung von fünf Komponenten“, häufig abgekürzt zu lnga-bsdus, bezeichnet.
6. Mittlere Umlaufzeiten von Sonne und Mond sowie der fünf Planeten Merkur, Venus, Mars, Jupiter und Saturn
Seit dem 15. Jahrhundert faszinierte es die Tibetischen Astronomen, die mittleren siderischen Umlaufzeiten (dkyil-'khor) sowie die mittleren Winkelgeschwindigkeiten (dus-longs) von Sonne, Mond und den fünf Planeten auf dem Sandabakus berechnen zu können. Dabei interessierte sie die mathematische Berechnung dieser Größen bezogen auf die drei Tagesarten (zhag -sum), nämlich Zodiak-Tag (khyim-zhag), lunarer Tag (tshes-zhag) und natürlicher Tag (nyin-zhag). Aus diesem Grund wurden diese Berechnungen auch zhag-gsum rnam-dbye „Analyse nach den drei Tagesarten genannt.“ Die Tibetischen Astronomen brauchten letztendlich mehrere Jahrhunderte, um die damit gegebenen arithmetischen Probleme der Kalkulationen mit mehrstelligen Zahlensystemen zufriedenstellend zu lösen.
Grundlegend für alle Kalkulationen war die Größenverhältnisse zwischen mittlerem Zodiak Tag und mittlerem lunaren Tag, nämlich
A= [1,2]/(-,65) = 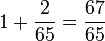 ,
,
und zwischen mittlerem lunarem Tag und natürlichem Tag, nämlich
B = 1 – [0,1,1]/(-,64,707) = 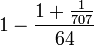 .
.
6.1. Die zeitlichen Längen von lunarem Tag und Zodiak-Tag
Zunächst interessierten sich die Tibetischen Astronomen für die zeitlichen Längen d in den astronomischen Zeiteinheiten lunarer Tag (tshes zhag) und Zodiak-Tag (khyim zhag).
Da per Definition die Länge eines natürlichen Tages 21600 Atemzüge (tib.: dbugs) beträgt, was [1,0,0,0,0]/(-,60,60,6,707) d entspricht, multipliziert man diesen Betrag mit
B= 1 – [0,1,1]/(-,64,707) = 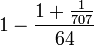 . Das Ergebnis, [0,59,3,4,16]/(-,60,60,6,707) d, ist die zeitliche Länge des lunaren Tages.
. Das Ergebnis, [0,59,3,4,16]/(-,60,60,6,707) d, ist die zeitliche Länge des lunaren Tages.
Zur Ermittlung der zeitlichen Länge des Zodiak-Tages multipliziert man dieses Ergebnis mit A = [1,2]/(-,65) =  . Das Ergebnis, [1,0,52,4,168, 50]/( -,60,60,6,707,65) d, ist die zeitliche Länge des Zodiak-Tages.
. Das Ergebnis, [1,0,52,4,168, 50]/( -,60,60,6,707,65) d, ist die zeitliche Länge des Zodiak-Tages.
6.2. Siderische Umlaufzeit und Winkelgeschwindigkeit der Sonne
Da per Definition die Umlaufzeit der Sonne (US,ZT) = 360 Zodiak Tage beträgt (nyi-ma´i khyim-zhag dkyil-´khor), ergibt 360 • A die Umlaufzeit der Sonne in mittleren lunaren Tagen (tib.: nyi-ma'i tshes-zhag dkyil-'khor):
US,LT = [371,4,36,5,7]/(-,60,60,6,13).
Multipliziert man dieses Ergebnis mit B, rechnet also 360 • A • B, so erhält man die Umlaufzeit der Sonne in natürlichen Tagen (nyi-ma'i nyin-zhag dkyil-'khor) :
US,d = [365,16,14,1]/(-, 60,60,6,13,707) d.
Dies ergibt als Länge des tropischen Jahres den Betrag 365,2705 d, was im Unterschied zur tatsächlichen Länge des tropischen Jahres von ca. 365,2422 eine Differenz von 0,0283 d bedeutet. Hieraus resultierte in Tibet eine Verschiebung des mittleren Jahresanfangs von 28,3 d, also von fast einem ganzen Monat, in tausend Jahren. Tatsächlich ergeben entsprechende Berechnungen, dass die Jahresanfänge in Tibet nach den auf dem Kālacakratantra basierenden Kalenderrechnungen im 11. Jahrhundert zwischen dem 1. Januar und dem 1. Februar schwankten, während sie im 20. Jahrhundert fast ausnahmslos in den Zeitraum Februar-März fielen.
Für die Berechnung der mittleren Winkelgeschwindigkeit, also der Veränderung der mittleren Länge der Sonne, bezogen auf die jeweiligen Zeiteinheiten Zodiak-Tag, lunarer Tag und natürlicher Tag, gibt Sanggye Gyatsho in seinem Vaiḍūrya dkar-po die allgemeine Regel an, das Winkelmaß für einen vollen Umlauf, d. s. 27 rgyu-skar (Mondhäuser) oder 27 • 60 = 1620 chu-tshod, durch die jeweilige Umlaufzeit eines Planeten zu dividieren. Wegen der arithmetischen Schwierigkeiten bei der Durchführung dieser Aufgabenstellung auf dem Sandabakus führt Sanggye Gyatsho die Rechenanweisungen für alle drei Tagesarten auf. Für die mittlere Winkelgeschwindigkeit der Sonne pro natürlichen Tag (nyi-ma'i nyin-zhag yul-longs) errechnet sich danach der Betrag
1620: US,d = [0,4,26,0,93,156]/(27,60,60,6,149,209) Mondhäuser.
Mittlere Winkelgeschwindigkeit der Sonne pro lunaren Tag (nyi-ma'i tshes-zhag yul-longs):
1620: US,LT = [0,4,21,5,43]/(27,60,60,67).
Multipliziert man diesen Betrag mit 30, erhält man die mittlere Länge des Bahnbogens, den die Sonne in einem synodischen Monat zurücklegt:
[2,10,58,1,17]/(27,60,60,6,67).
6.3. Umlaufzeit und Winkelgeschwindigkeit des Mondes
Nach einem synodischen Monat erreicht der Mond in der Ekliptik die Position der Sonne. Die mittlere Winkelgeschwindigkeit des Mondes pro synodischem Monat errechnen die tibetischen Astronomen damit, dass sie zum Winkelmaß eines vollen Umlaufs (27 • 60 = 1620 chu-tshod) den mittleren Bahnbogen addieren, den die Sonne in einem synodischen Monat zurücklegt. Das Ergebnis dividiert man durch 30 und erhält somit die Winkelgeschwindigkeit des Mondes pro lunarem Tag (zla-ba'i tshes-zhag yul-longs):
[0,58,21,5,43]/(27,60,60,6,67).
Zur Berechnung der Umlaufzeit des Mondes in lunaren Tagen (zla-ba'i tshes-zhag dkyil-'khor) dividiert man das Winkelmaß eines vollen Umlaufs durch die Winkelgeschwindigkeit pro lunarem Tag und erhält als Ergebnis
UM,LT = [27,45,21,4,430]/-,60,60,6,869).
Multipliziert man dieses Ergebnis mit B, also dem oben erwähnten Umrechnungsfaktor von lunaren Tagen in natürliche Tage, so erhält man die Umlaufzeit des Mondes in natürlichen Tagen:
UM,d = [27, 279,37,1250]/(-,869,64,1414) d.
Dieser Wert für die Umlaufzeit des Mondes entspricht 27,32166 d und ist im Vergleich zum exakten Wert 27,321674 d sehr genau.
Für die Winkelgeschwindigkeit des Mondes pro natürlichem Tag errechnen die tibetischen Astronomen den Betrag
[0,59,17,3,95367]/(27,60,6,149209) Mondhäuser.
6.4.Untere und obere Planeten
Grundsätzlich unterscheidet man in der tibetischen Astronomie zwischen sogenannten „friedlichen Planeten“ (zhi-gza´), dies sind die unteren Planeten Merkur (lhag-pa) und Venus (pa-sangs), und den „gewalttätigen Planeten“ (drag-gza´), dies sind die oberen Planeten Mars (mig-dmar), Jupiter (phur-bu) und Saturn (spen-pa).
Diese Unterscheidung erklärt sich aus der modernen Astronomie dadurch, dass bei den inneren Planeten Merkur und Venus der Radius der Umlaufbahn um die Sonne kleiner als der der Erde ist, während die Radien der Umlaufbahnen der äußeren Planeten Mars, Jupiter und Saturn größer als der Radius der Umlaufbahn der Erde sind.
Die tibetische Astronomie kennt diese physikalische Erklärung dieser Gruppierung nicht. Sie orientiert bei dieser Unterscheidung an den Beobachtung, dass die „friedlichen Planeten“ (unteren Planeten) von der Erde aus gesehen zwar der Sonne vorhereilen oder ihr nachlaufen, dass dieser Winkelabstand zur Sonne aber niemals einen vollen Umlauf in der Ekliptik (360°) ausmacht. Tatsächlich ist dieser Winkelabstand zur Sonne bei der Venus maximal etwa 45° und beim Merkur maximal etwa 20°.
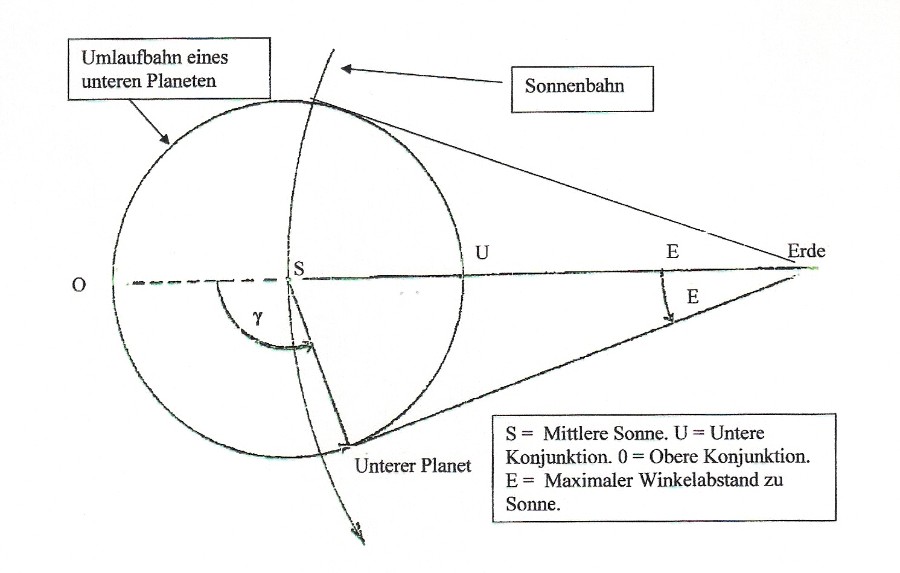
Während die unteren Planeten von der Erde ausgesehen also gleichsam um die Sonne hin- und herpendeln, ist bei den „gewalttätigen Planeten“ (oberen Planeten) die Situation völlig anders, da sie von der Erde aus gesehen in Opposition zu Sonne stehen können, also zur Sonne einen Winkelabstand von 180° erreichen.
6.5. Umlaufzeiten der Planeten Merkur, Venus, Mars, Jupiter und Saturn
Für die siderischen Umlaufzeiten der 5 Planeten Merkur (lhag-pa), Venus (pa-sangs) , Mars (mig-dmar) , Jupiter (phur-bu) und Saturn (spen-pa) wurden die entsprechenden Werte aus dem Kālacakratantra übernommen und in der Folgezeit nicht mehr geändert. Diese sind:
Untere Planeten
- Merkur 87,97 d (Exakter Wert 87,969 d).
- Venus 224,7 d (Exakter Wert 224,701 d).
Obere Planeten
- Mars 687 d (Exakter Wert 686,98 d).
- Jupiter 4.332 d (Exakter Wert 4.332,59 d)
- Saturn 10.766 d (Exakter Wert 10.759,21 d)
Diese Werte sind bis auf eine unwesentliche Abweichung beim Saturn erstaunlich genau.
Die Umrechnung dieser Größen in Datumstage und Zodiak-Tage und die Errechnung der entsprechenden Winkelgeschwindigkeiten erfolgt analog zu dem Verfahren, das zu den entsprechenden Werten der Sonne beschrieben wurde.
7. Mittlere ekliptikale, heliozentrische Längen der Planeten Merkur, Venus, Mars, Jupiter und Saturn
Auf der Grundlage eines Weltbildes, nach dem die Planeten einschließlich Sonne und Mond um einen Weltberg kreisen, letztendlich also die Erde im Mittelpunkt der Bewegung der Planeten steht, ergibt die Berechnung von heliozentrischen Längen der Planeten eigentlich keinen Sinn. Hier werden nämlich Positionen, berechnet, bei denen die Sonne im Mittelpunkt stehen muss. Die tibetischen Astronomen geben hierzu keine Erklärung und folgen einfach den nach ihrer Tradition von Buddha gelehrten Berechnungen des Kālacakratantra.
7.1. Zahl der seit Epoche vergangenen natürlichen Tage
Zur Berechnung der mittleren, heliozentrischen Länge eines Planeten ermittelt man nach dem Kālacakratantra zunächst die Zahl der seit Epoche vergangenen natürlichen Tage. Dazu multipliziert man die Zahl der vergangenen lunaren Monate L(J,M) mit 30 und addiert die Zahl der vergangenen lunaren Tage T. Letzteres ist die Datumszahl, mit der ein Wochentag innerhalb eines Monats gezählt wird. Damit erhält man die Zahl der seit Epoche vergangenen lunaren Tage. Zur Umrechnung dieses Wertes in natürliche Tage verwenden alle Schulen der Tibetischen Astronomie wieder den Umrechnungsfaktor B = 1 – [0,1,1]/(-,64,707) = 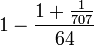 .Spätere Schulen der Astronomie addieren zu der Zahl der vergangenen lunaren Tage im Subtrahenden noch einen bestimmten Betrag D. Dieser gibt mit
.Spätere Schulen der Astronomie addieren zu der Zahl der vergangenen lunaren Tage im Subtrahenden noch einen bestimmten Betrag D. Dieser gibt mit 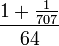 multipliziert die Tageszeit an, zu der erste lunare Tag in dem betreffenden Wochentag beginnt. Da dieser Betrag subtrahiert wird, verschiebt man mit 1 – D •
multipliziert die Tageszeit an, zu der erste lunare Tag in dem betreffenden Wochentag beginnt. Da dieser Betrag subtrahiert wird, verschiebt man mit 1 – D • 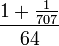 den Anfang der Berechnung der Zahl der vergangenen natürlichen Tage genau auf die Epoche, d. i. der Beginn des 1. Wochentages des 1. Monats des 1. Jahres. Das Ergebnis
den Anfang der Berechnung der Zahl der vergangenen natürlichen Tage genau auf die Epoche, d. i. der Beginn des 1. Wochentages des 1. Monats des 1. Jahres. Das Ergebnis
Tageszahl = 
ist die sogenannten unklare (mi-gsal) Zahl der seit Epoche vergangenen natürlichen Tage (nyin-zhag gi grangs oder spyi-zhag). Sie ist deshalb unklar, weil Sie den Fehler aufweist, dass in ihr die durch die Unregelmäßigkeiten des Umlaufs von Sonne und Mond bedingten Veränderungen der Längen von lunaren Tagen nicht berücksichtigt sind. Aus diesem Grunde addiert man den Wochentag aus dem Anfangswert WA(m) und teilt das Ergebnis durch 7. Das Ergebnis vergleicht man mit dem aktuellen Wochentag des Kalenders und korrigiert die oben errechnete Tageszahl um die Differenz zwischen dem aktuellen Wochentag und dem errechneten Wochentag.
Die später vorgenommene Ergänzung durch die Addition von D im Subtrahenden, die im Kālacakratantra nicht vorkommt, ist insofern hyperkorrekt, als sie wegen der anschließenden mathematischen Korrektur zahlenmäßig keinerlei Auswirkung hat.
7.2. Anfangswerte
Bei den Planeten werden die zur Epoche vorgegebenen Anfangswerte (Anf), d. s. die Abweichungen der Längen der Himmelskörper vom Nullpunkt des ekliptikalen Umlaufs, nicht im Winkelmaß der Mondhäuser angegeben sondern durch die Zahl der Tage (d), die der einzelne Planet benötigt hat, um nach Durchlauf durch den Nullpunkt der Ekliptik seine Länge zum Zeitpunkt der Epoche zu erreichen. Als Epoche wird hier die des Kālacakratantra, d. i. der Beginn des Nag-Monats des Jahres 806, verwendet.
Liste der Anfangswerte der fünf Planeten:
7.3. Mittlere heliozentrische Längen der fünf Planeten
Zu der oben ermittelten Tageszahl addiert man für jeden Planeten den Anfangswert und teilt das Ergebnis durch die Umlaufzeit. Der Rest dieser Division gibt für jeden Planeten die Zahl der Tage, die seit dem Durchlauf des jeweiligen Planeten durch den Nullpunkt der Ekliptik vergangen sind (sgos-zhag):
 .
.
Da sich diese Zahl zur vollen Umlaufzeit genauso verhält, wie die im Winkelmaß angegebene mittlere Länge eines Planeten zum Winkelmaß des vollen Umlaufs in der Ekliptik (= 27), ergibt sich für jeden Planeten als Winkelmaß für die mittlere Länge:

Für die drei oberen Planeten (drag-gza´) wird dieser Betrag als „mittlere Länge der langsamen Bewegung der drei oberen Planeten bezeichnet“ (drag-gsum dal-bar). Für die beiden unteren Planeten wird dieser Betrag „Eingangswert der Mittelpunktsgleichung der beiden unteren Planeten“ (zhi-gnyis rkang-´dzin) genannt. Für die Sonne wird dieser Betrag als nyin-zhag nyi-bar bezeichnet.
8. Die langsamen Füße der Planeten: siderische Mittelpunktsgleichungen zur Berechnung der exakten heliozentrischen Länge
Da sich die Planeten nicht auf einer Kreisbahn, sondern sich annähernd auf einer Ellipse um die Sonne bewegen, variiert ihre Winkelgeschwindigkeit. Diese unterschiedlichen Winkelgeschwindigkeiten führen dazu, dass die tatsächlichen ekliptikalen heliozentrischen Längen dieser Himmelskörper von den berechneten mittleren Längen abweichen. Die mathematische Formel, mit der man diese Abweichungen von der mittleren Länge berechnet, nennt man Mittelpunktsgleichungen. In der graphischen Darstellung ergibt sich aus diesen Gleichungen jeweils eine trigonometrische Kurve.
Bezüglich des Mondes und der Sonne wurden die Mittelpunktsgleichungen im Kontext der Tibetischen astronomischen Kalenderrechnung ausführlich dargestellt. Siehe hierzu Mittelpunktsgleichung des Mondes und Mittelpunktsgleichung der Sonne.
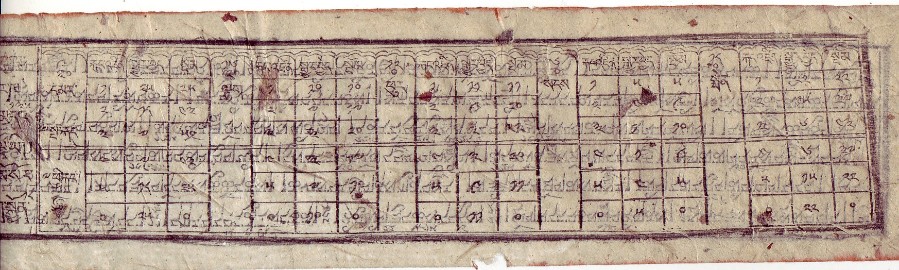 |
Tibetische Tafel der Mittelpunktsgleichungen der fünf Planeten Merkur, Venus, Mars, Jupiter und Saturn |
Da die Berechnung der Mittelpunktsgleichungen der restlichen fünf Planeten, die langsame Füße genannt werden (dal-rkang), bei entsprechender Aufteilung der Ekliptik in zwölf Abschnitte analog zu den Berechnungen der Mittelpunktsgleichung der Sonne durchgeführt wurde, genügt es hier, die Längen der Nullpunkte der anomalistischen Umläufe und die Interpolationstafeln aufzuführen.
Nullpunkte, Aphel und Perihel der anomalistischen Umläufe der Planeten:
| Planet | Nullpunkt des anomalistischen Umlaufs in Mondhäuser | Sonnenfernster Punkt (Aphel) in Mondhäuser | Sonnennächster Punkt (Perihel) in Mondhäuser | Sonnennächster Punkt nach Kālacakratantra in Grad | Tatsächlicher Wert (Perihel) 500 n. Chr. | Tatsächlicher Wert (Perihel) 1900 n. Chr. |
| Merkur | [16,30]/(27,60) | [23,15]/(27,60] | [9,45]/(27,60) | 130 Grad | 144,1 Grad | 165,9 Grad |
| Venus | [6,0]/(27,60) | [12,45]/(27,60] | [26,15]/(27,60) | 350 Grad | 290,5 Grad | 310,2 Grad |
| Mars | [9,30]/(27,60) | [16,15]/(27,60] | [2,45]/(27,60) | 36,66 Grad | 38,5 Grad | 64,2 Grad |
| Jupiter | [12,0]/(27,60) | [18,45]/(27,60] | [5,15]/(27,60) | 70 Grad | 80,2 Grad | 102,7 Grad |
| Saturn | [18,0]/(27,60) | [24,45]/(27,60] | [11,15]/(27,60) | 150 Grad | 153,7 Grad | 181,1 Grad |
Tafel für die Mittelpunktsgleichungen der fünf Planeten:
| | n: Zugriffsnummern der Gleichungen (rkang-´dzin) | Mars: Steigung der Funktion oder Multiplikator (sgyur-byed) | Mars: Anfangswerte der Funktionen (rkang-sdom) | Merkur: Steigung der Funktion oder Multiplikator (sgyur-byed) | Merkur: Anfangswerte der Funktionen (rkang-sdom) | Jupiter: Steigung der Funktion oder Multiplikator (sgyur-byed) | Jupiter: Anfangswerte der Funktionen (rkang sdom) | Venus: Steigung der Funktion oder Multiplikator (sgyur-byed) | Venus: Anfangswerte der Funktionen (rkang-sdom) | Saturn: Steigung der Funktion oder Multiplikator (sgyur-byed) | Saturn: Anfangswerte der Funktionen (rkang-sdom) |
|---|
| Erste Hälfte der Gleichungen (snga-rkang): Zu addierende Beträge. | 1 | 25 | 25 | 10 | 10 | 11 | 11 | 5 | 5 | 22 | 22 |
| Erste Hälfte der Gleichungen (snga-rkang): Zu addierende Beträge. | 2 | 18 | 43 | 7 | 17 | 9 | 20 | 4 | 9 | 15 | 37 |
| Erste Hälfte der Gleichungen (snga-rkang): Zu addierende Beträge. | 3 | 7 | 50 | 3 | 20 | 3 | 23 | 1 | 10 | 6 | 43 |
| Zweite Hälfte der Gleichungen (phyi-rkang): Zu subtrahierende Beträge. | 4 | -7 | 43 | -3 | 17 | -3 | 20 | -1 | 9 | -6 | 37 |
| Zweite Hälfte der Gleichungen (phyi-rkang): Zu subtrahierende Beträge. | 5 | -18 | 25 | -7 | 10 | -9 | 11 | -4 | 5 | -15 | 22 |
| Zweite Hälfte der Gleichungen (phyi-rkang): Zu subtrahierende Beträge. | 0 | -25 | 0 | -10 | 0 | -11 | 0 | -5 | 0 | -22 | 0 |
Bei den Rechnungen mit diesen Mittelpunktsgleichungen gibt es einen wesentlichen Unterschied zwischen den oberen und den unteren Planeten. Bei den oberen Planeten korrigiert man mit diesen Gleichungen jeweils die mittlere Länge (dal-bar) des betreffenden Planeten.
Bei den unteren Planeten korrigiert man mit den Werten aus den Mittelpunktsgleichungen für Merkur und Venus jeweils separat die Länge der mittleren Sonne am Ende des betreffenden natürlichen Tages (nyin-zhag nyi-bar).
Das Ergebnis wird in allen Fällen „korrekte langsame Länge“ (dal-ba dag-pa) des betreffenden Planeten bezeichnet, obwohl es bei den unteren Planeten sich jeweils eigentlich um mittlere Länge der Sonne handelt, die mit den Mittelpunktsgleichungen von Merkur und Venus korrigiert wurde.
9. Die schnellen Füße der fünf Planeten: Berechnung der geozentrischen Abweichungen der Längen der Planeten
Eine weitere Korrektur der mittleren Länge eines Planeten, die in der tibetischen Astronomie nach Berücksichtigung der Mittelpunktsgleichungen berechnet wird, beruht auf dem Umstand, dass sich für einen Beobachter auf der Erde die Bewegung der Erde in der scheinbaren Bewegung der Planeten gleichsam spiegelt.
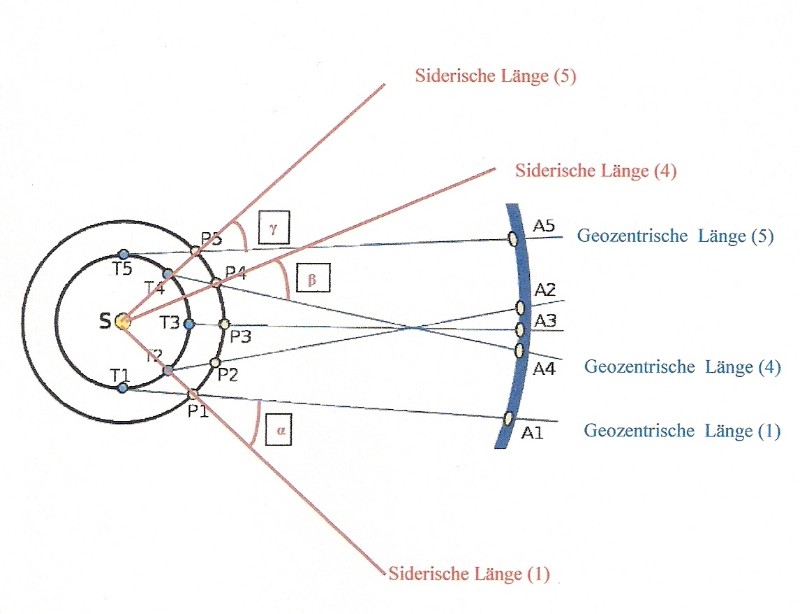
|
Darstellung der geozentrischen Länge eines oberen Planeten |
Auf der vorstehenden Abbildung kennzeichnen S die Sonne und der innere Kreis die Umlaufbahn der Erde um die Sonne. Die Punkte T1 – T5 geben die Position der Erde zu bestimmten, unterschiedlichen Zeitpunkten wieder. Der zweite Kreis um die Sonne S sei die Umlaufbahn eines oberen Planeten und die Punkte P1 – P5 sollen die Positionen dieses oberen Planeten zu den Zeitpunkten wiedergeben, an denen sich die Erde an den Punkten T1 – T5 befindet.
Die schwarze Linie von T1 durch P1 gibt von der Erde aus gesehen in A1 die Position des oberen Planeten am Himmelsgewölbe wieder. Befindet sich die Erde danach am Punkt T2 und der obere Planet gleichzeitig in der Position P2, so befindet sich der obere Planet von der Erde aus gesehen am Punkt A2. Der Planet hat sich also von der Erde aus gesehen ( im Bild gegen den Uhrzeigersinn) von A1 nach A2 vorwärtsbewegt. Entsprechend befindet sich danach vom Punkt T3 aus gesehen der obere Planet (P3) am Punkt A3. Anschließend, von T4 aus gesehen, befindet sich der Planet (P4) in der Position A4. Aus der Sicht eines Beobachters auf der Erde hat sich der Planet also nun von Erde aus gesehen von A2 nach A3 und anschließend nach A4 (im Bild im Uhrzeigersinn) gleichsam rückwärts bewegt, um sich danach wieder gegen den Uhrzeigersinn nach A5 vorwärts zu rücken. Die von der Erde aus beobachteten Positionen A1 – A5 erfassen wir mit dem Begriff geozentrische Länge.
Zeichnet man auf der oben stehenden Abbildung Geraden (hier nur drei Geraden, rot eingezeichnet) vom Mittelpunkt der Erdbahn (Sonne) durch die Planetenpositionen P1 bis P5, so ergeben sich an den Schnittpunkten P1 bis 5 der Planetenpositionen Winkel, die die Abweichung der geozentrischen Längen A1 bis A5 von den berechneten heliozentrischen (siderischen) Längen beschreiben. In der Abbildung wurden nur die Geraden vom Mittelpunkt der Erdbahn (=Sonne) für die Punkte P1, P4 und P5 eintragen. Der Winkel α gibt an, dass die mittlere heliozentrische Länge bei der Position 1 des äußeren Planeten um diesen Winkel kleiner ist als die von der Erde aus beobachte Länge am Punkt A1. Der Winkel β gibt an, dass die mittlere heliozentrische Länge bei der Position P4 des äußeren Planeten um diesen Winkel größer ist als die von der Erde aus beobachte Länge am Punkt A4. Der Winkel γ gibt an, dass die mittlere heliozentrische Länge bei der Position P5 des äußeren Planeten um diesen Winkel größer ist als die von der Erde aus beobachte Länge am Punkt A5.
In der tibetischen Astronomie werden diese Abweichungen mit einem System linearer Gleichungen berechnet, die man „schelle Füße“ (myur-rkang) nennt. Tibetische Werke zur Astronomie enthalten Tafeln mit den Anfangswerten und Steigungen dieser Gleichungen, mit denen man die Abweichung der geozentrischen Längen von den siderischen Längen berechnet. Die Eingangs- bzw. Zugriffswerte zu diesen Gleichungen sind bei den oberen Planeten die Winkel, die sich aus der Differenz zwischen der mittleren Länge der Sonne am Ende des natürlichen Tages (nyin-zhag nyi-bar) und der exakten heliozentrischen Länge der Planeten (drag-gsum dal-dag) errechnen. Bei den unteren Planeten Merkur und Venus errechnet sich dieser Zugriffswinkel, indem man von den mittleren heliozentrischen Längen dieser beiden Planeten (zhi-gnyis rkang-´dzin) die um die Mittelpunktsgleichungen der unteren Planeten korrigierte Länge der Sonne (zhi-gnyis dal-dag) abzieht. Mit den Werten, die sich aus diesen Gleichungen errechnen, werden die zuvor berechneten exakten heliozentrischen Längen (dal-dag) korrigiert.
Die Berechnungsmethode beruht vollständig auf den Angaben des Kālacakratantra und wurde von den tibetischen Astronomen nicht verändert. Es ist davon auszugehen, dass die zur Berechnung verwendeten Werte rein empirisch aus längeren Beobachtungsreihen gewonnen wurden.
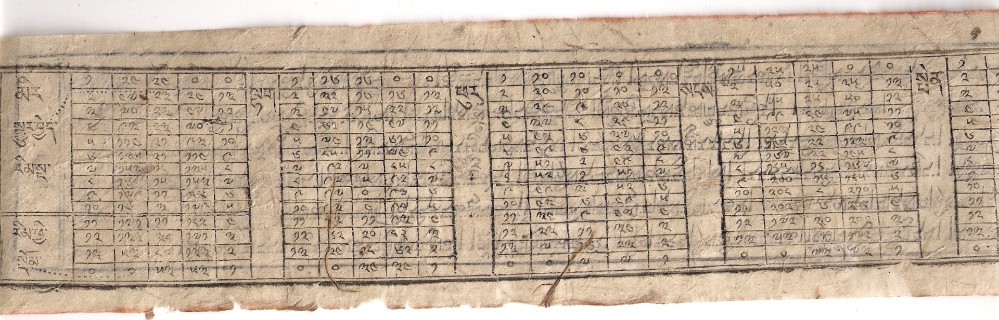 |
Tibetische Tafel zur Berechnung der geozentrischen Abweichungen der ekliptikalen Längen der Planeten |
10. Literatur
Kālacakratantra. (Tibetisch) mChog gi dang-po sangs-rgyas las phyung-ba rgyud kyi rgyal-po dus kyi 'khor-lo.
Grags-pa rgyal-mtshan: Dus-tshod bzung-ba'i rtsis-yig
karma Nges-legs bstan-'dzin: gTsug-lag rtsis-rigs tshang-ma'i lag-len 'khrul-med mun-sel nyi-ma ñer-mkho'i 'dod-pa 'jo-ba'i bum-bzang (Blockdruck).
Phug-pa Lhun-grub rgya-mtsho: Legs par bshad pa padma dkar-po´i zhal gyi lung. Beijing 2002
sde-srid Sangs-rgyas rgya-mtsho: Phug-lugs rtsis kyi legs-bshad mkhas-pa'i mgul-rgyan vaidur dkar-po'i do-shal dpyod-ldan snying-nor (Blockdruck)
sde-srid Sangs-rgyas rgya-mtsho: bsTan-bcos vaiḍūrya dkar-po las dri-lan 'khrul-snang g.ya'-sel don gyi bzhin-ras ston-byed (Blockdruck)
Nag-dbang: sNgon med-pa'i bstan-bcos chen po vaiḍūrya dkar-po las 'phros-pa'i snyan-sgron nyis-brgya brgyad-pa (Blockdruck)
Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig Maximilians Universität zu München. München 1966
Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973
Dieter Schuh: Grundzüge der Entwicklung der Tibetischen Kalenderrechnung. Zeitschrift der Deutschen Morgenländischen Gesellschaft, Supplement II. XVIII. Deutscher Orientalistentag vom 1. bis 5. Oktober 1972 in Lübeck. Vorträge, S. 554-566
Autor: Dieter Schuh, 2010. Bildnachweise: Darstellungen der Welt mit Weltberg von Daniel Kränert (Halle).





