Astronomiegeschichte (Tibet)

Die Geschichte der Tibetischen Astronomie (skar-rtsis) ist die Darstellung der Entwicklung einer im historischen Tibet verbreiteten Wissenschaft (rig-gnas; „Ort des Wissens“) über den Aufbau der Erde und des Weltalls, über die Errechnung der Struktur und der Bestandteile des tibetischen astronomischen Kalenders, über die Berechnung der Bewegung der in Tibet bekannten zehn Planeten einschließlich Sonne und Mond sowie des Kometen Encke und über die Berechnung von Sonnen- und Mondfinsternissen. Durchgeführt wurden die astronomischen Berechnungen mit dem tibetischen Sandabakus.

Die Tibetische Astronomie ist indischen Ursprungs, da sie auf den astronomischen Lehren des ersten Kapitels des Kālacakratantra beruht, eines indischen tantrischen Lehrtexts, dessen Sanskrit-Textversion nicht vor 1027 entstanden sein kann und der in der 2. Hälfte des 11. Jahrhunderts erstmals ins Tibetische übersetzt wurde. 

Inhaltsverzeichnis

1. Ursprung nach mythologischer buddhistischer Tradition
2. Übersetzung ins Tibetische
3. Anfänge der Herausbildung einer eigenen Wissenschaft der Astronomie in Tibet (12. Jahrhundert und Beginn des 13. Jahrhunderts)
4. Erste astronomische Lehrbücher tibetischer Autoren (2. Hälfte des 13. Jahrhunderts)
5. Kommentierung der Programmtexte der praktischen Rechenbücher (14. Jahrhundert
6. Die Entstehung und Entwicklung der eigenständigen Tibetischen Astronomie (grub-rtsis)
7. Literatur

1. Ursprung nach mythologischer buddhistischer Tradition

Nach tibetischer Überlieferung wurde das tantrische Lehrsystem Kālacakra, „Rad der Zeit“, vom historischen Buddha kurz vor oder nach seinem Tod an dem südindischen Stūpa von Dhānyakaṭaka vor einer mythischen Zuhörerschaft auf Bitten von Sucandra (Zla-ba bzang-po), einem König des sagenhaften Königreiches Shambhala, gelehrt. Sucandra soll diese Lehren in einem 12.000 Verse umfassenden, Wurzel-Tantra (rTsa-rgyud, Mūlatantra) genannten Werk niedergeschrieben haben. Das von Sucandra verfasste Wurzel-Tantra soll jedoch, bis auf einige Zitate in späteren Werken, verloren gegangen sein.

Jamyang Drag, König von Shambhala und Verfasser des Kālacakratantra		Pema Karpo, König von Shambhala und Verfasser des Kommentarwerks Vimalaprabhā

Der für die Entwicklung der tibetischen Astronomie maßgebliche Text ist das erste Kapitel des als Kālacakratantra bekannten Werkes, das einem anderen mythischen König von Shambhala, nämlich Jamyang Dragpa ('Jam-dbyangs grags-pa), zugeschrieben wird und eine verkürzte Version des verlorengegangenen Wurzel-Tantra sein soll. Der tibetische Titel dieses Werkes lautet: mChog gi dang-po sangs-rgyas las phyung-ba rgyud kyi rgyal-po dus kyi 'khor-lo („Der von Buddha, dem ersten der Allerhöchsten, offenbarte König der Tantras, das Rad der Zeit“).

Die tantrische Gottheit vom Rad der Zeit		Sucandra, König von Shambhala, empfängt die Kālacakra-Unterweisungen

Die verwendeten Rechengrößen zur Erleichterung der praktischen Durchführung der Rechnungen sind in solch einem Werk verkürzt bzw. aufgerundet. So wird beispielsweise zur Vereinfachung der Rechnungen mit weniger Zahlen hinter dem Komma gerechnet als exakt erforderlich wäre. Die praktischen Rechenbücher sind vor dem Hintergrund großer systematischer indischer Abhandlungen über astronomische Rechnungen entstanden die Siddhānta genannt werden, und in denen mit komplizierteren Zahlenwerten und langen Zeitperioden gerechnet wird. Für den täglichen Gebrauch wurde dies nicht als notwendig erachtet.

Aus Sicht der Wissenschaftsgeschichte der indischen Astronomie hat der astronomische Inhalt des Kālacakratantra deshalb keine herausragende Bedeutung. Das erste Kapitel des Kālacakratantra diente jedoch dazu, einen Großteil des sehr weit entwickelten astronomischen Wissens der Inder nach Tibet zu exportieren, wo es mit der Bewertung, autoritative Verkündung des historischen Buddha zu sein, eine hohe Wertschätzung und eine eigentümliche Weiterentwicklung erfuhr.

Astrologische Inhalte finden sich im ersten Kapitel des Kālacakratantra so gut wie gar nicht.

Von großer Bedeutung für die Entwicklung der tibetischen Astronomie war das Kommentarwerk Vimalaprabhā („Makelloser Glanz“) zum Kālacakratantra, das ebenfalls einem mythischen König von Shambhala, nämlich Pema Karpo (tib.: padma dkar-po), dem Nachfolger Jamyang Dragpas, zugeschrieben wurde.

Dieses Kommentarwerk enthält zahlreiche Zitate aus dem Wurzel-Tantra, die für die spätere Entwicklung der tibetischen Astronomie bedeutsam waren. Dem Verfasser der Vimalaprabhā sind folgenschwere Fehleinschätzungen bei der Kommentierung zuzuschreiben, die aus einer offenkundigen Unkenntnis des Verhältnisses von Karaņa- und Siddhānta Werken der indischen Astronomie resultierten. So findet sich in der Vimalaprabhā der Hinweis, Ungläubige hätten die im Wurzel-Tantra enthaltene wahre, vom Buddha gelehrte Astronomie in böswilliger Absicht verfälscht und diese Verfälschungen im ersten Kapitel des Kālacakratantra verbreitet.

Diese Hinweise sowie die Angabe einiger für korrekt gehaltener abweichender Werte aus dem Wurzel-Tantra, waren ein wesentlicher Antrieb für die Entwicklung der tibetischen Astronomie, die sich letztendlich als 'Rekonstruktion der wahren, von Buddha gelehrten Siddhānta-Astronomie' verstand und im Tibetischen als Grub rtsis bezeichnet wurde.

Die Vimalaprabhā stellt insbesondere zwei Werte heraus, die für die Astronomie des Wurzel-Tantra wesentlich gewesen sein sollen. Der eine Wert ist der Faktor zur Umrechnung der Länge eines mittleren solaren Monats (khyim-zla) bzw. eines mittleren Zodiak-Tages (khyim-zhag) in mittlere lunare Monate (tshes-zla) bzw. mittlere lunare Tage (tshes-zhag), der mit

A =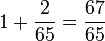

angegeben werden kann. Dieser Wert besagt, dass 67 mittleren synodischen bzw. lunaren Monaten 65 solare Monate entsprechen.

Der zweite Umrechnungsfaktor betrifft das Verhältnis der zeitlichen Länge eines mittleren lunaren Tages zu der zeitlichen Länge eines natürlichen Tages (nyin-zhag). Hiernach entspricht einem mittleren lunaren Tag

B =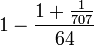

natürliche Tage.

2. Übersetzung ins Tibetische

Das Kālacakratantra wie auch die Vimalaprabhā stammen in ihrer vorliegenden Fassung aus dem 11. Jahrhundert. Beide Werke wurden in der zweiten Hälfte des 11. Jahrhunderts von dem indischen Gelehrten Somanātha und dem tibetischen Übersetzer Drolo Sherab Drag ('Bro-lo Shes-rab grags) ins Tibetische übersetzt.

3. Die Anfänge der Herausbildung einer eigenen Wissenschaft der Astronomie in Tibet (12. Jahrhundert und Beginn des 13. Jahrhunderts)

Die Überlieferung indischen astronomischen Wissens im Rahmen des tantrischen Meditationszyklus Kālacakratantra nach Tibet hatte zunächst weder irgendeine Bedeutung für den tibetischen Kalender noch bewirkte sie eine nennenswerte Beschäftigung von Tibetern mit Fragen der komplizierten Berechnungen der indischen Astronomie. Hierzu bedurfte es der Herauslösung des astronomischen Wissens aus dem Tantrazyklus Kālacakra und der Darstellung in eigenen astronomischen Texten.

Diese Aufgabe übernahmen im 11. und zu Beginn des 12. Jahrhunderts wiederum zwei an der Astronomie interessierte indische buddhistische Gelehrte, die in Tibet an der Verbreitung des Buddhismus mitwirkten.

Der erste dieser beiden Gelehrten war Abhayākaragupta (1084–1130), in Tibet unter dem Namen Lobpön (slob-dpon ,„Lehrmeister“) Abhaya bekannt, der unter dem Titel Kālacakrāvatāra die astronomischen Inhalte des Kālacakratantra in einer eigenständigen Abhandlung darstellte und anschließend an der Übersetzung dieses Werkes ins Tibetische durch den Nyinphugpa Chökyi Dragpa (Nyin-phug-pa Chos kyi grags-pa) (1094-1186) mitwirkte.

 Der zweite dieser beiden Gelehrten war der berühmte kaschmirische Gelehrte Śakyaśrībhadra (1127–1225), der drei auf den Lehren des Kālacakratantra basierende Schriften zur Astronomie verfasste, in denen er die Kalenderrechnung, die Berechnung der Sonnen- und Mondfinsternisse und der Bewegung der fünf Planeten Merkur, Mars, Venus, Jupiter und Saturn behandelte. Śakyaśrībhadra besuchte Tibet im Jahre 1204 und hielt sich dort bis 1214 auf.

Er wurde einer der herausragenden Lehrer des Sakya Paṇḍita Künga Gyeltshen (Kun-dga´ rgyal-mtshan) (1182–1251). Aus der Biographie Sakya Paṇḍita Künga Gyeltshens ist zu entnehmen, dass er eine gründliche praktische Ausbildung zur Kalenderrechnung und Astronomie des Kālacakratantra absolviert hat. Er war somit der erste der Sakya-Hierarchen, von dem wir wissen, dass er eine solche Ausbildung erhalten hatte.

Zu dieser Ausbildung gehörte unter anderem die praktische Durchführung der Addition, Subtraktion, Division und Multiplikation mittels des Sandabakus, die Berechnung der fünf Komponenten der Kalenderrechnung, die Berechnung von Sonnen- und Mondfinsternissen, der Längen der 5 Planeten und der Position des Kometen Encke. Eigene Beiträge zur tibetischen Astronomie und Kalenderrechnung wurden von Sakya Paṇḍita nicht verfasst

Nyinphugpa Chökyi Dragpa, tibetischer Übersetzer des Kālacakrāvatāra		Sakya Paṇḍita, Schüler des Śakyaśrībhadra. Er war einer der ersten tibetischen Gelehrten, die eine gründliche praktische Ausbildung in Astronomie absolvierten.

4. Erste astronomische Lehrbücher tibetischer Autoren (2. Hälfte des 13. Jahrhunderts)

Angesicht des zunehmenden Interesses an der rechnenden Astronomie entstanden bald erste Lehrbücher tibetischer Autoren zu diesem Thema. Der erste tibetische Autor, von dem uns solche Schriften vorliegen, war der berühmte tibetische Geistliche Chögyel Phagpa (chos-rgyal ´Phags-pa),  1235–1280).

Chögyel Phagspa verfasste neun Abhandlungen zur Kalenderrechnung und Astronomie. In allen Fällen handelt es sich hierbei um praktische Rechenbücher. Die Abhandlungen Chögyel Phagpas sind die ältesten der uns bisher bekannten Darstellungen der Kālacakra-Astronomie in tibetischer Sprache, die keine Übersetzungen aus dem Indischen darstellen. Inhaltlich folgt Chögyel Phagpa noch weitgehend den Darlegungen des Kālacakratantra.

Der auf dem Kālacakratantra basierende Kalender wurde durch ihn in Tibet eingeführt und als der maßgebliche, von Buddha gelehrte Kalender etabliert. Insofern legte Chögyel Phagpa politisch die Basis für die spätere eigenständige Entwicklung der tibetischen Astronomie und Kalenderrechnung.

 Ein weiterer bedeutender Geistlicher, der zur Verbreitung des astronomischen Wissens in Tibet beitrug, ist der 3. Karmapa Rangjung Dorje (Rang-byung rdo-rje) (1284–1339). Rangjung Dorje verfasste 1318 das erste von zwei Lehrbüchern, die die Astronomie und Kalenderrechnung sowie die Astrologie behandeln.

Auch die Lehrbücher des Rangjung Dorje sind praktische Rechenbücher, die voll in der Tradition des Kālacakratantra stehen und somit wissenschaftsgeschichtlich im Vergleich zu den Werken von Chögyel Phagspa bis auf eine Ausnahme wenig Neues bieten. Auf ca. 4 ½ Seiten erläutert er rechnerisch verkürzte Berechnungen zu der mittleren Bewegung von Sonne, Mond, der Planeten und der Mondknoten. Dies ist der früheste bisher bekannt gewordene Versuch, die Umlaufzeiten dieser Himmelskörper bzw. die mittlere Veränderung ihrer ekliptikalen Längen pro bestimmter Zeiteinheit zu berechnen. Hervorzuheben sind auch seine Darlegungen zu den Sonnen- und Mondfinsternissen und seine Berechnungen zur Sichtbarkeit des Kometen Encke. Außerdem etablierte er mit seinen beiden Abhandlungen die Kālacakra-Astronomie und Kalenderrechnung in der Kagyü(bka´-brgyud)-Schule. Zur inhaltlichen Weiterentwicklung der tibetischen Astronomie, leistete er noch keinen nennenswerten Beitrag.

Chögyel Phagpa, einer der ersten tibetischen Verfasser autochtoner tibetischer Schriften zur Astronomie und Kalenderrechnung		Karmapa Rangjung Dorje, er verfasste 1318 sein erstes Lehrbuch zur tibetischen Astronomie

5. Kommentierung der Programmtexte der praktischen Rechenbücher (14. Jahrhundert)

Die praktischen, in Versen geschriebenen Rechenbücher der sich in Tibet allmählich ausbreitenden Astronomie waren allesamt Programmtexte mit Rechenanweisungen für den Sandabakus, die kaum Erklärungen darüber abgaben, was eigentlich warum berechnet wurde. Hierzu bedurfte es bis zum Beginn des 14. Jahrhunderts der mündlichen Unterweisung eines Lehrers. Dies änderte sich auch für die Darstellungen in den späteren praktischen Rechenbüchern bis in die Neuzeit nicht. Um die Problematik deutlich zu machen wird im Folgenden der im Zusammenhang mit den Rechnungen mit dem Sandabakus vorgestellte Programmtext noch einmal erläutert, wobei die interpretierenden Begriffe aus der Astronomie durch die wörtliche Bedeutung der tibetischen Bezeichnungen ersetzt wurden:

  "(1.) Platziere die „reine Monatszahl“ auf fünf Stellen. 

(2.) Von oben multipliziere nacheinander mit „Auge“ (2), „Himmelsrichtung“ (10), „Schlangengott Sinnesorgan“ (58), „Körper“ (1), „Mond Planet“ (17).

(3.) Von oben addiere nacheinander „Sosein“ (25), „Schatz“ (8), „Null Körper“ (10), „Veden“ (4), „Zähne“ (32).

(4.) Nach oben Umrechnung durch die Stellenwerte „Berg Geschmack“ (67), „Jahreszeit“ (6), „Himmel Geschmack“ (60), „Null Zwischenhimmelsrichtung“ (60), „Rad“ (27).

(5.) Der Rest, nach Löschen der höchsten Stelle, ist die mittlere Sonne."

 Dem tibetischen Schüler der Astronomie wurde von seinem Lehrer mündlich erklärt, was „reine Monatzahl“, nämlich die Zahl der zuvor errechneten vergangen synodischen Monate, oder was „mittlere Sonne“, nämlich „mittlere Länger der Sonne am Ende des betreffenden synodischen Monats“, bedeutet, in den praktischen Rechenbüchern findet sich dazu aber keine Erklärung. Das Gleiche gilt für die Bedeutung der Zahlengrößen, die nach der obigen Rechenvorschrift zu addieren oder zu multiplizieren sind.

Die erste umfassende Erklärung der astronomischen Inhalte der astronomischen Rechenbücher lieferte einer der bekanntesten Gelehrten des tibetischen Mittelalters, nämlich Butön Rinchen Drub (Bu-ston Rin-chen grub). Butön verfasste mehrere Werke zur Astronomie und Kalenderrechnung. Hervorzuheben ist insbesondere das erste große in Prosa geschriebene Kommentarwerk zur Kālacakra-Astronomie und Kalenderrechnung mit dem Titel „Lehrbuch über die Kalkulationen des Kālacakra, etwas, das die Gelehrten erfreut“ (dPal dus kyi 'khor-lo'i rtsis kyi bstan-bcos mkhas -pa rnams dga'-bar byed-pa) welches er am 14. November 1326 fertigstellte.

Mit diesem Werk, das 244 Seiten umfasst, liegt die erste bisher bekannt gewordene Abhandlung zur Astronomie und Kalenderrechnung vor, die nicht die bloße Form eines praktischen Rechenbuches hat, sondern im großen Umfang versucht, den Sinn der durchzuführenden Rechenoperationen zu erklären. Insofern war Butöns Werk bahnbrechend für die systematische Entwicklung der Tibetischen Astronomie und der tibetischen Kalenderrechnung.

Butön waren die zahlenmäßigen Verkürzungen im Kālacakratantra und deren Deutung als böswillige Verfälschungen durch die Vimalaprabhā sehr gut bekannt. Entsprechend finden sich bei ihm auch erste Versuche, in Anlehnung an die übermittelten sogenannten „wahren Werte“ neue Rechnungsmethoden einzuführen. Gelungen ist ihm dies letztendlich nicht, da er die mathematischen Schwierigkeiten der entsprechenden arithmetischen Rechnungen mit dem Sandabakus nicht lösen konnte.

6. Die Entstehung und Entwicklung der eigenständigen Tibetischen Astronomie (grub-rtsis)  

 Siehe die Hauptartikel: Phugpa-Schule der Tibetischen Astronomie und Thurphu-Schule der Tibetischen Astronomie

Die im Kālacakratantra enthaltenen astronomischen Berechnungen entsprechen dem, was in zahlreichen praktischen Rechenbüchern der indischen Astronomie und Kalenderrechnung üblicherweise dargestellt wurde. In Sanskrit werden solche Rechenbücher Karaņa bzw. später im Tibetischen byed-rtsis („Praktisches Rechnen“) genannt. Die verwendeten Rechengrößen wurden zur Erleichterung der praktischen Durchführung der Rechnungen in solchen Werken verkürzt bzw. aufgerundet.

Ausgangspunkt der Entwicklung einer eigenständigen tibetischen Astronomie war die in dem kanonischen Text Vimalaprabhā, einem Kommentar zum Kālacakratantra, verbreitete These, Ungläubige hätten die wahre, vom Buddha gelehrte und in einem verlorengegangenen Wurzel-Tantra (rtsa-rgyud) aufgezeichnete Astronomie in böswilliger Absicht verfälscht und diese Verfälschungen im ersten Kapitel des Kālacakratantra verbreitet.

  Die Aufgabenstellung der tibetischen Astronomen wurde somit von ihnen selbst letztendlich als „Rekonstruktion der wahren, von Buddha gelehrten Siddhānta-Astronomie“ verstanden, die im Tibetischen als grub-rtsis bezeichnet wurde. Beobachtungen des Sternhimmels waren eigentümlicher Weise für die Entwicklung dieser Astronomie ohne nennenswerte Bedeutung.

Im 15. Jahrhundert bildeten sich in Tibet verschiedene Schultraditionen der Astronomie heraus. Die bekanntesten von ihnen waren die Phugpa-Schule, benannt nach ihrem Gründer  Phugpa Lhündrub Gyatsho (Phug-pa Lhun-grub rgya-mtsho) und die Tshurphu-Schule (mTshur-lugs), benannt nach den Kloster Tshurphu (mTshur-phu).

Infolge der intensiven Beschäftigung mit der Astronomie und der Kalenderrechnung entstanden in Tibet zahlreiche Werke zur Astronomie, von denen die wichtigsten als Blockdrucke veröffentlicht wurden. Zu erwähnen ist hier insbesondere der Vaiḍūrya dkar po des Regenten Desi Sanggye Gyatsho (sde-srid Sangs-rgyas rgya-mtsho).

Für die Entwicklung der tibetischen Astronomie und Kalenderrechung bedeutende Persönlichkeiten waren unter Anderen Chögyel Phagpa, Butön Rinchen Drub, Phugpa Lhündrub Gyatsho, Norsang Gyatsho (Nor-bzang rgya-mtsho), Pelgön Thrinle (dPal-mgon ´phrin-las), Tshurphu Jamyang Chenpo Döndrub Öser (mTshur-phu ´jam-dbyangs chen-po Don-grub ´od-zer), der Regent Sanggye Gyatsho, Karma Ngeleg Tendzin (karma Nges legs bstan 'dzin) und der Nyingma-Gelehrte Lochen Dharmaśrī (1654–1717).

7. Literatur

Winfried Petri: Indo-tibetische Astronomie. Habilitationsschrift zur Erlangung der venia legendi für das Fach Geschichte der Naturwissenschaften an der Hohen Naturwissenschaftlichen Fakultät der Ludwig Maximilians Universität zu München. München 1966.
Dieter Schuh: Untersuchungen zur Geschichte der Tibetischen Kalenderrechnung. Wiesbaden 1973.
Dieter Schuh: Grundzüge der Entwicklung der Tibetischen Kalenderrechnung. Zeitschrift der Deutschen Morgenländischen Gesellschaft, Supplement II. XVIII. Deutscher Orientalistentag vom 1. bis 5. Oktober 1972 in Lübeck. Vorträge, S. 554-566.
Zuiho Yamaguchi: Chronological Studies in Tibet. Chibetto no rekigaku: Annual Report of the Zuzuki Academic foundation X, S. 77-94 1973.
Zuiho Yamaguchi: The Significance of Intercalary Constants in the Tibetan Calender and Historical Tables of Intercalary Month. Tibetan Studies: Proceedings of the 5th Seminar of the International Association for Tibetan Studies, Vol. 2, pp. 873-895 1992.
sde-srid Sangs-rgyas rgya-mtsho: Phug-lugs rtsis kyi legs-bshad mkhas-pa'i mgul-rgyan vaidur dkar-po'i do-shal dpyod-ldan snying-nor (Blockdruck).
karma Nges-legs bstan-'dzin: gTsug-lag rtsis-rigs tshang-ma'i lag-len 'khrul-med mun-sel nyi-ma nyer-mkho'i 'dod-pa 'jo-ba'i bum-bzang (Blockdruck).
Phug-pa Lhun-grub rgya-mtsho: Legs par bshad pa padma dkar-po´i zhal gyi lung. Beijing 2002.

Autor: Dieter Schuh, 2010. Bildnachweise:1. Kālacakra: Sujit Kumar, Wikimedia Commons http://commons.wikimedia.org/wiki/File:Kala_Chakra.jpg?uselang=de 2. Sakya Pandita: John Hill, Wikimedia Commons http://commons.wikimedia.org/wiki/File:Sakya_Pandita.jpg?uselang=de 3. Chögyel Phagpa: Miuki, Wikimedia Commons http://commons.wikimedia.org/wiki/File:Chogyal.JPG?uselang=de 4. Karmapa Rangchung Dorje: Wikimedia Commons http://commons.wikimedia.org/wiki/File:Karmapa3.jpg?uselang=de 5. Buton Rinchen Drub: Blofeld of Spectre, Wikimedia Commons http://de.wikipedia.org/w/index.php?title=Datei:ButonRinchen.jpg&filetimestamp=20080818143140 Alle übrigen Abbildungen nach Vaiḍūrya dkar po